ეს უნდა იცოდეთ

სამი GIF, რომელიც სკოლაში აუცილებლად უნდა ეჩვენებინათ რიცხვ პის ახსნისას

დღეს, 14 მარტს, მსოფლიოში რიცხვ პის დღე აღინიშნება. მიზეზი მარტივია — მესამე თვის რიცხვი 14.

π-ს შესახებ ალბათ გსმენიათ და ისიც იცით, რომ წრეწირის სიგრძის მის დიამეტრთან შეფარდების ტოლია. ყველამ, ვინც სკოლაში ოდნავ ყურადღებას მაინც უთმობდა გაკვეთილებს იცის, რომ მისი მნიშვნელობა 3,14-ს უდრის; შედარებით ცოტას ახსოვს, რომ უფრო ზუსტად იგი 3,14159-ია; ხოლო დანარჩენებს, ყურმოკრული მაინც აქვთ, რომ სინამდვილეში, ეს რიცხვი საერთოდ არ მთავრდება და უსასრულო რაოდენობის ციფრებისგან შედგება.

წარმოგიდგენთ 3 GIF-ს, რომელიც ყველაზე მარტივად აგიხსნით, რა არის და საიდან მოდის პი.

GIF #1

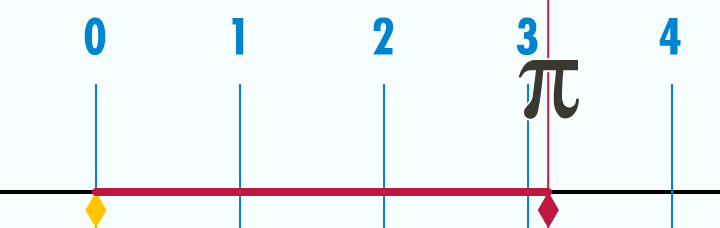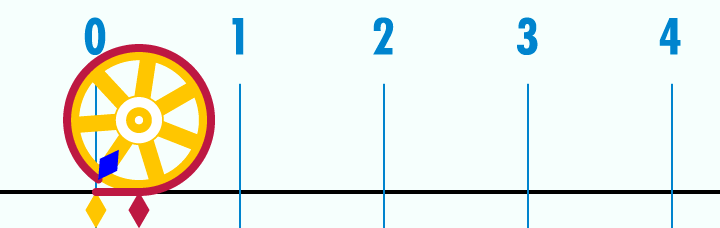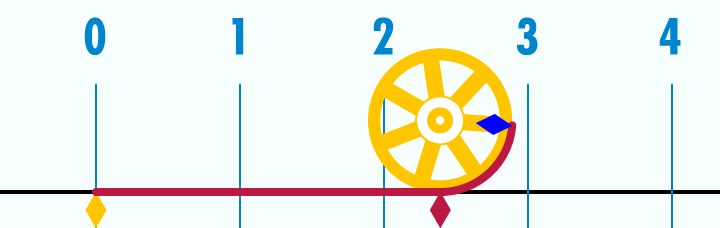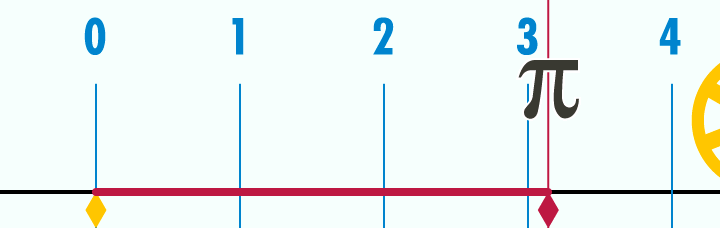
ფოტო: Wikipedia

რადგან π წრეწირის სიგრძის და დიამეტრის შეფარდებაა, თუკი ავიღებთ ერთეულოვან წრეწირს (ანუ წრეწირს, რომლის დიამეტრი 1 პირობითი ერთეულის ტოლია) და გავშლით მას წრფეზე, ერთეული სიგრძის დიამეტრი ამ მონაკვეთში 3-ზე ცოტა მეტჯერ უნდა ჩაეტიოს. უფრო ზუსტად კი — 3,14-ჯერ. კიდევ უფრო ზუსტად კი... 3,14159-ჯერ. საბოლოო სიზუსტით ამ რიცხვს ვერასდროს დავწერთ, რადგან, როგორც უკვე აღვნიშნეთ, ის არასოდეს მთავრდება.

GIF #2

ფოტო: Nerdist

მეორე გზა, რომლითაც π-ს გააზრება შეგვიძლია, კუთხის საზომი ერთეული — რადიანია. ერთი რადიანი არის წრის ორ რადიუსს შორის არსებული კუთხე, რომლის შესაბამისი რკალის სიგრძეც, თავად ამ რადიუსების ტოლია. თუკი გავზომავთ, ვნახავთ, რომ ნახევარ წრეში 3 ცალი რადიანი და კიდევ სულ ცოტა (0,14159…) ეტევა. დაკვირვებულები უკვე შეამჩნევდით, რომ ეს რიცხვი ზუსტად იმდენია, რამდენი დიამეტრიც ჩაეტია ზემოთ, წრის სიგრძეში :)

ეს გასაკვირი არ არის, რადგან როგორც ვიცით, წრის რადიუსი, მისი დიამეტრის ნახევარია. ხოლო განმარტებასაც თუ გავიხსენებთ, მარტივად მივხვდებით, რომ ამ შემთხვევაშიც, ნახევარ წრეში პი-ცალი რადიანი ჩაეტევა.

GIF #3

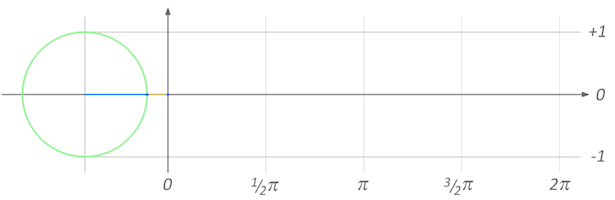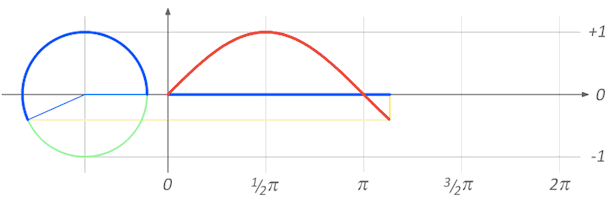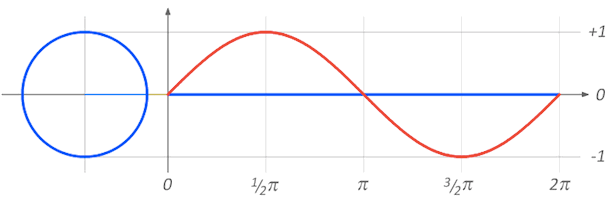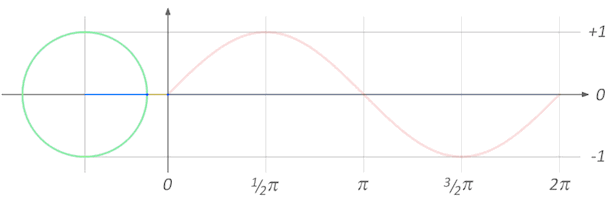
მესამე მეთოდი, რომლითაც წრის გარშემოწერილობის და მისი დიამეტრის შეფარდების სხვაგვარად წარმოდგენა შეგვიძლია, სინუსოიდაა. დახატული და მოციმციმე სინუსოიდა, სავარაუდოდ, ხშირად გინახავთ სამეცნიერო ფანტასტიკურ ფილმებში, ან, სამედიცინო დაწესებულებებში, ან, შეიძლება, სკოლაშიც კი, ტრიგონომეტრიის სწავლისას. სინუსოიდა სინუს-ფუნქციის აღმწერი ორგანზომილებიანი გრაფიკია. ეს ფუნქცია კი, რეალურად, ძალიან მარტივი რამეა — მართკუთხა სამკუთხედში, ჩვენთვის საინტერესო მახვილი კუთხის მოპირდაპირე კათეტის შეფარდება ჰიპოტენუზასთან (ანუ ის გვერდი, რომელიც მართკუთხა სამკუთხედში ყველაზე გრძელია).

როგორც ზედა GIF-დან ჩანს, სინუსოიდა ასევე შეგვიძლია წარმოვადგინოთ, როგორც კოორდინატები ერთეულოვან წრეწირზე და, როგორც კი ნახევარ წრეწირს „გავირბენთ”, ზუსტად π მანძილი გვექნება „გავლილი” სინუსოიდის აბსცისთა ღერძზე.

და ბოლოს — თუ ძალიან ცნობისმოყვარე ხართ და გაინტერესებთ, რა ციფრები მოდის 3,14-ის შემდეგ, ინებეთ პის პირველი ათასი სიმბოლო ათწილადის ნიშნის შემდეგ:

3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989

წყარო:https://on.ge/story/8810-%E1%83%A1%E1%83%90%E1%83%9B%E1%83%98-gif-%E1%83%A0%E1%83%9D%E1%83%9B%E1%83%94%E1%83%9A%E1%83%98%E1%83%AA-%E1%83%9C%E1%83%94%E1%83%A2%E1%83%90%E1%83%95-%E1%83%A1%E1%83%99%E1%83%9D%E1%83%9A%E1%83%90%E1%83%A8%E1%83%98-%E1%83%94%E1%83%A9%E1%83%95%E1%83%94%E1%83%9C%E1%83%94%E1%83%91%E1%83%98%E1%83%9C%E1%83%90%E1%83%97-%E1%83%A0%E1%83%98%E1%83%AA%E1%83%AE%E1%83%95-%E1%83%9E%E1%83%98-%E1%83%A1-%E1%83%90%E1%83%AE%E1%83%A1%E1%83%9C%E1%83%98%E1%83%A1%E1%83%90%E1%83%A1

იაპონელმა ქალმა რიცხვ პის მსოფლიო რეკორდი მოხსნა

პი, როგორც იცით, მათემატიკის სამყაროში ერთ-ერთი ყველაზე პოპულარული რიცხვია. მისი მნიშვნელობა წრეწირის სიგრძის მისივე დიამეტრთან შეფარდების ტოლია. ხშირად ამბობენ, რომ პი 3,14-ს უდრის, სინამდვილეში კი პი უსასრულო რიცხვია, რომელიც უსასრულო რაოდენობის ციფრებისგან შედგება.

ემა ჰარუკა ივაო გუგლის თანამშრომელია, რომელმაც პის მნიშვნელობა 31 ტრილიონ ციფრამდე გამოთვალა და ამ დრომდე არსებული 22-ტრილიონიანი რეკორდი მოხსნა.

არსებული ციფრების გაგრძელება ძალიან რთულია, რადგან პის მიმდევრობა რაიმე კანონზომიერებას არ ექვემდებარება.

პი ინჟინერიაში, ფიზიკაში, კომპიუტერებსა და კოსმოსურ ხომალდებში გამოიყენება, მისი საშუალებით შესაძლებელია ტალღებთან, წრეებთან და ცილინდრებთან დაკავშირებული გამოთვლების ჩატარება.

ემა ჰარუკა ივაომ ციფრების გამოსათვლელად გუგლის ქლაუდ სისტემა გამოიყენა, რომელიც 170 ტერაბაიტ ინფორმაციას 121 დღის განმავლობაში ამუშავებდა.

"მე სასიამოვნოდ გაკვირვებული ვარ. აღნიშნული რეკორდის მოხსნა ძალიან რთული იყო. ვიცით, რომ პის დასასრული არ აქვს, მაგრამ მისი ციფრების გამოთვლას სიამოვნებით გავაგრძელებდი", - აცხადებს ის.

31,4-ტრილიონიანი ციფრის მქონე რიცხვის წარმოსათქმელად 332 064 წელი იქნებოდა საჭირო.

NASA-ს გამოქვეყნებული აქვს სია, სადაც ჩამოთვლილია, თუ რაში იყენებს კოსმოსური სააგენტო რიცხვ პის, მაგალითად, ნასა მისი საშუალებით ითვლის მარსის ხომალდებისათვის საჭირო პარაშუტის ზომას. პის საშუალებით ხდება იმის გამოთვლაც, თუ რამდენი კვადრატული ფორმის სურათი იქნება საჭირო თანამგზავრიდან პლანეტის ზედაპირის სრულად გადასაღებად. პი გამოიყენება პლანეტების გარშემო არსებულ ორბიტებზე ხომალდების გასანთავსებლადაც.

"თანამედროვე მათემატიკა, ფიზიკა, ინჟინერია და ტექნოლოგია პის გარეშე ვერ იფუნქციონირებდა", - აცხადებს მათემატიკოსი მეთ პარკერი.

2010 წელს ნიკოლას ზემ Yahoo-ს ქლაუდ კომპიუტერების გამოყენებით გამოითვალა, რომ პის მეორეკვადრილიონე ციფრი ნული იყო, აღნიშნულ გამოთვლას ჩვეულებრივ კომპიუტერზე 500 წელიწადი დასჭირდებოდა. 

წყარო: BBC

''ოქროს კვეთა '' მუსიკაში

''ოქროს კვეთა '' მუსიკაში

                      „მუსიკა-ბგერის ხელოვნებაა... ბგერა,მუსიკის მა 

                                 ტერია, გახვეული უნდა იყოს სიჩუმეში,განისვე

                                   ნოს მასში , როგორც ძვირფასმა თვალმა ხავერ

                             დოვან ზარდახშაში.“,-ამბობდა ჰენრიხ ნეიგჰაუზი.

              

                                      

ოქროს კვეთა გამოყენებული აქვთ:
ბეთჰოვენს , ჰაიდნს, მოცარტს, შოპენს , შუბერტს და სხვა
კლასიკოსებს.;ბეთჰოვენს-97%,ჰაიდნს-97%, მოცარტს-91%,
შოპენს-92%,შუბერტს-91%.

ლუდვიკ ვან ბეთჰოვენის სონეტებში ოქროს კვეთა გამოყენებულია
დამუშავებაში, სადაც მთავარი თემა მუშავდება და იცვლება
ტონალობაში. თვითონ დამუშავება გაყოფილია ორ დიდ
ნაწილად მისი I, VI და XVIII ტაქტები კი დაკავშირებულია
ოქროს კვეთით.

სამოდელო გაკვეთილი "ორ წერტილს შორის გამოთვლა"

2019 წლის 28  თებერვალს  სსიპ ქ. ქუთაისის N21 საჯარო სკოლის მე-8 კლასში ჩავატარე პრობლემაზე ორიენტირებული   სამოდელო გაკვეთილი მათემატიკაში .

ამ ტიპის  გაკვეთილის ჩატარება განაპირობა იმ გარემოებამ, რომ ის განსაკუთრებით ზრდის მოსწავლის მოტივაციას. მოსწავლე ჩართულია აქტიურ სწავლაში, მუშაობს რეალური პრობლემის გადაჭრაზე, რის შედეგადაც სწავლა მისთვის უფრო საინტერესო და სახალისო ხდება. ზრდის მის პასუხისმგებლობას სწავლისადმი;

მოსწავლეებში ავითარებს კრიტიკულ აზროვნებას. პრობლემის გადაჭრაზე ფიქრისას მოსწავლე კრიტიკულად აფასებს, რა იცის, რა უნარ-ჩვევები აქვს და რა სჭირდება პრობლემის გადასაჭრელად. ამყარებს მიმართებას რამდენიმე ცნებას შორის და გამოაქვს დასკვნა

ავითარებს შემოქმედებით აზროვნებას. პრობლემის გადაჭრაზე მუშაობის დროს მოსწავლეს შეიძლება მოუხდეს პრობლემის გადაჭრის რამდენიმე შესაძლებლობის განხილვა, ან პრობლემის გადაჭრის რამდენიმე პასუხის პოვნა, ან ახალი (ორიგინალური) გზის ძიება.

ასეთი სწავლება ორიენტირებულია მოსწავლეებში პირობისეული, ანუ ფუნქციური ცოდნის შეძენაზე.

 თემის აქტუალობას განსაზღვრავდა ის გარემოება,რომ:  ყოველდღიურ ყოფა-ცხოვ რებაში ხშირად  ვაწყდებით  პრობლემებს, რომლის გადაჭრა შეგვიძლია თეორი ულ ად ნასწავლი ცოდნის გამოყენებით. მოსწავლეთათვის აუცილებელია ერთ ვითარე ბაში ნასწავლი ცოდნის გადატანა სხვა სიტუაციაში, თეორიული მასალის სწავლის საჭიროების დანახვა რეალური სიტუაციებიდან, ყოელდღიური ცხოვრებიდან გამო მ დინარე, მაგალითად, სასურველ ობიექტამდე მისვლა ძნელდება და ხშირად შეუძლე ბელიც არის ბუნებრივი დაბრკოლებების გამო / შენობები, მდინარეები, დედამიწის რელიეფური ზედაპირი/ , როდესაც გადავადგილდებით ერთი პუნქტიდან მეორეში, რეალურად განვლილი მანძილი მეტია, ვიდრე უმოკლესი, ორ პუნქტს შორის მან ძილი, რომლის ცოდნასაც მოითხოვს ცხოვრებისეული სიტუაციები.

გაკვეთილის მიზნს წარმოადგენდა, მათემატიკური ცოდნის, კერძოდ, პითაგორას თე ორემის, ორ წერტილს შორის  მანძილის გამოსათვლელი ფორმულის გამოყენებით მანძილის გამოთვლა რეალურ ვითარებაში.

გაკვეთილი დავიწყე ისეთი პრობლემის განხილვით , რომელიც მოსწავლეებისათვის აქტუალური იყო, პრობლემის ამოცანის შინაარსმა მოსწავლეებში  აღძრა ინტერესი.

პრობლემური სიტუაცია დავუკავშირე საკლასო გარემოს და ყოვედღიურ საყოფაცოვრებო  სიტუაციას ,აპლიკაციის საშუალებით,  ამოცანა იყო რეალური და

  იძლეოდა ცოდნისა და გამოცდილების ინტეგრირების შესაძლებლობას. პრობლემა ფოკუსირებულად მივმართე   ერთ საკითხზე, მანძილის გამოვლაზე. მოსწავლეებს მივეცი საკმარისი დრო,  პრობლემის გადაჭრისათვის საჭირო ინფორმაციის შეგროვებისაა და შესაბამისი სტრატეგიების შერჩევად.

გაკვეთილი წარიმართა გეგმის შესაბამისად, არ მომიხდენია  დაგეგმილი აქტივობების და დროის ცვლილება.  გაკვეთილი იყო საინტერესო, მაგრამ ვთვლი , რომ ცოდნის კონსტრუირება B ფაზაზე აქტივობამ,  ''პრობლემის გადაწყვეტის გზების ძიება'',რომლის მიზანის წარმოადგენდა; შეძენილი ცოდნის პრაქტიკული გამოყენება კეთებით ,დიდად  განაპირობა გაკვეთილის წარმატება.

მოსწავლეები გამოთქვამდნენ პრობლემის გადასაჭრელად   მოსაზრებებს,  მე, მასწავლებელი ვაწარმოებდი სკაფოლდინგის, ვსვამდი  პრობლემის  გარშემო,   დამაზუსტებელ კითხვებს; რათა კლასი მიმეყვანა ალტერნატიული გზებით პრობლემის გადაჭრისკენ.

 სახალისო და საინტერესო იყო, მოსწავლეების  მიერ იატაკზე  პრაქტიკულად წარმოადგენენ იმ მართკუთხა სამკუთხედის, რომლის ჰიპოტენუზა კარადიდან მაგიდამდე მანძილია ,გაზომვა  ამ  მართკუთხა სამკუთხედის კათეტების რულეტის საშუალებით,  იატაკზე   მოთავსებული მართკუთხა კორდინატთა სისტემის  გამოყენება, მოსწავლეების მიერ წერტილის კოორდინატების როლის შესრულება. მოსწავლეებმა იოლად განახორციელეს ცოდნის ტრანსფერი, დაინახეს  თეორიის და პრაქტიკის კავშირი და ეს ტრანსფერი თავად განახორციელეს კეთებით, რამაც განაპირობა საგაკვეთილო მიზნის მიღწევა.

ჩატარებულმა გაკვეთილმა, კიდევ ერთხელ დამარწმუნა იმაში რომ , თეორიული ცოდნა, თუ ის არ იქნა გააზრებული და შესაბამისად გამოყენებული პრაქტიკაში, არაფრის მომცემია.

 კეთებით სწავლის მეთოდი ამ გაკვეთილისთვის იყო უნივერსალური, გამოიწვია ინტერესი, გაზარდა ჩართულობა, ამ აქტივობის დროს აბსოლიტურად ყველას ინტერესს იწვევდა საგაკვეთილო პროცესი და მასში მონაწილეობის მიღება.მოსწავლეთა შეფასება მოვახდინე  როგორც განმსაზღვრელი, ასევე განმავითარებელი შეფასებით, წინასწარ შედგენილი რუბრიკის გამოყენებით, მაგრამ ვთვლი რომ, რადგან ძალიან მაღალი იყო აქტივობა და მოსწავლეთა ჩართულობა, შემეძლო უფრო მეტი განმსაზღვრელი  ქულის დაწერა. მოსწავლეებმა გაკვეთილი შეაფასეს "შუქნიშნის" პრინციპით დარიგებული ფერადი სტიკერების საშუალებით.               კმაყოფილი ვარ ,რომ მოლოდინმა გაამართლა, მივაღწიე არა მარტო საგაკვეთილო მიზანს, არამედ დავაინტერესე მოსწავლეები  ნასწავლი ცოდნა გამოიყენონ პრაქტიკაში .